Bạn có thể đã nghe nói về khả năng biến Python thành một công cụ tính toán mạnh mẽ, thậm chí là máy tính khoa học hay máy tính đồ thị chuyên nghiệp. Với sự hỗ trợ của các thư viện phong phú, Python vượt xa vai trò của một ngôn ngữ lập trình thông thường, trở thành một giải pháp miễn phí và linh hoạt cho mọi nhu cầu tính toán, từ cơ bản đến phức tạp, giúp bạn “bỏ xó” chiếc máy tính cầm tay truyền thống.
Bài viết này sẽ đi sâu vào cách tận dụng Python cùng các thư viện phổ biến như math, SymPy, NumPy và statistics để thực hiện hàng loạt các phép toán, từ số học cơ bản, lượng giác, giải phương trình đại số, thống kê cho đến vẽ đồ thị hàm số, khẳng định vị thế của Python như một “công cụ toán học” không thể thiếu cho sinh viên, kỹ sư và bất kỳ ai làm việc trong lĩnh vực khoa học, công nghệ.
Khai Thác Tiềm Năng Toán Học Với Các Thư Viện Python
Python được trang bị một bộ sưu tập thư viện khổng lồ, là chìa khóa để mở khóa khả năng tính toán vượt trội của nó. Mỗi thư viện được thiết kế để xử lý một loại tác vụ toán học cụ thể, đảm bảo độ chính xác và hiệu quả cao:
- Thư viện
math: Cung cấp các hàm toán học tiêu chuẩn như lượng giác, logarit, lũy thừa, căn bậc hai và các hằng số toán học. Đây là lựa chọn đầu tiên cho các phép tính toán học cơ bản đến trung bình. - Thư viện
SymPy: Một thư viện mạnh mẽ cho toán học tượng trưng (symbolic mathematics). Nó cho phép bạn làm việc với các biểu thức đại số, giải phương trình (kể cả phương trình vi phân) và thực hiện các phép tính vi tích phân mà không cần thay thế biến bằng giá trị số cụ thể. SymPy đặc biệt hữu ích khi bạn cần kết quả chính xác dưới dạng biểu thức, không phải xấp xỉ số. - Thư viện
NumPy: Viết tắt của “Numerical Python”, NumPy là nền tảng cho khoa học dữ liệu và tính toán số trong Python. Nó cung cấp các cấu trúc dữ liệu mảng hiệu quả và một bộ sưu tập lớn các hàm toán học để thực hiện các phép toán trên mảng và ma trận, cực kỳ nhanh chóng và hiệu quả. NumPy là xương sống cho nhiều thư viện tính toán và phân tích khác. - Thư viện
statistics: Cung cấp các hàm cơ bản cho thống kê mô tả, như tính toán giá trị trung bình, trung vị, mode, độ lệch chuẩn, phương sai, v.v. Nó giúp đơn giản hóa việc phân tích dữ liệu nhanh chóng.
Bằng cách kết hợp các thư viện này, Python trở thành một môi trường tính toán toàn diện, mạnh mẽ và hoàn toàn miễn phí, có thể thay thế nhiều phần mềm thương mại đắt tiền.
Thực Hiện Các Phép Tính Lũy Thừa, Căn Bậc N và Logarit
Lũy thừa, căn bậc N và logarit là những phép toán cơ bản nhưng rất quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Python cung cấp các toán tử và hàm chuyên dụng để thực hiện chúng một cách dễ dàng và chính xác.
Tính Lũy Thừa
Để nâng một cơ số lên lũy thừa N, bạn chỉ cần sử dụng toán tử **. Ví dụ, để tính 2 mũ 2:
2**2Lưu ý rằng nhiều ngôn ngữ hoặc phần mềm khác như Excel sử dụng ký hiệu ^ (caret) cho lũy thừa. Việc này có thể gây nhầm lẫn nếu bạn đã quen với chúng. Hãy đảm bảo bạn sử dụng toán tử ** để tránh lỗi cú pháp trong Python.
Tính Căn Bậc N
Đối với căn bậc hai, thư viện math cung cấp hàm sqrt().
import math
math.sqrt(81)Đây sẽ trả về kết quả là 9. Đối với các số không phải là số chính phương, hàm này sẽ trả về giá trị xấp xỉ thập phân, tương tự như máy tính khoa học. Ngoài ra, hàm math.cbrt() hoạt động tương tự cho căn bậc ba.
Python tính toán căn bậc hai sử dụng hàm `sqrt` từ thư viện `math`
Để tính căn bậc cao hơn 3 (ví dụ, căn bậc N của X), bạn có thể sử dụng toán tử lũy thừa với số mũ là 1/N. Ví dụ, để tính căn bậc tám của 256:
256**(1/8)Dấu ngoặc đơn (1/8) là rất quan trọng. Nếu không có chúng, Python sẽ hiểu là 256 mũ 1, sau đó chia kết quả cho 8, điều này không phải là mục đích của chúng ta. Với dấu ngoặc, phép tính sẽ trả về 2, vì 2 mũ 8 bằng 256.
Tính Logarit
Logarit là phép toán ngược của lũy thừa. Hàm math.log() trong Python cho phép bạn tính logarit của một số với một cơ số nhất định. Mặc định, nó sử dụng logarit tự nhiên (ln) với cơ số e (khoảng 2.71828…):
math.log(42)Để sử dụng logarit thập phân (log cơ số 10), bạn cung cấp cơ số làm đối số thứ hai:
math.log(42, 10)Thư viện math cũng cung cấp một hàm tắt tiện lợi cho logarit thập phân, do đây là loại logarit rất phổ biến:
math.log10(42)Logarit cơ số 2 cũng rất phổ biến trong lĩnh vực điện toán và tin học. Python có một hàm tương tự với cơ số 2, giúp bạn dễ dàng xác định số bit cần thiết để biểu diễn một số:
math.log2(512)Nếu bạn cần tính logarit với một cơ số bất kỳ khác, bạn có thể sử dụng công thức chuyển đổi cơ số logarit: log_b(x) = log_e(x) / log_e(b) hoặc log_b(x) = log_10(x) / log_10(b). Ví dụ, để tính logarit của 81 với cơ số 3:
math.log(81) / math.log(3)Phép tính này sẽ trả về 4, vì 3 mũ 4 bằng 81. Bạn có thể kiểm tra lại bằng cách tính antilogarit:
3**4Sử Dụng Hằng Số Toán Học và Hàm Lượng Giác
Thư viện math không chỉ cung cấp các hàm mà còn có sẵn các hằng số toán học quan trọng như e (số Euler) và pi (số Pi), cùng với các hàm lượng giác cần thiết.
Hằng Số Toán Học
Hằng số math.pi và math.e có thể được sử dụng trực tiếp trong các phép tính. Ví dụ, để tính diện tích hình tròn có bán kính 6 đơn vị (công thức: diện tích = Pi * bán kính^2):
import math
math.pi * 6**2Hàm Lượng Giác
Thư viện math cung cấp các hàm lượng giác cơ bản như sin (sin), cosin (cos), tang (tan) cũng như các hàm lượng giác ngược tương ứng (arcsin asin, arccos acos, arctan atan).
Các hàm lượng giác trong Python hoạt động với đơn vị radian. Nếu bạn có góc bằng độ, bạn cần chuyển đổi chúng sang radian bằng hàm math.radians(). Ví dụ, để chuyển đổi 60 độ sang radian:
import math
math.radians(60)Để tính sin của góc này:
angle = math.radians(60)
math.sin(angle)
Ví dụ minh họa cách sử dụng hàm `sin` cho tính toán lượng giác trong Python với thư viện `math`
Bạn có thể lấy lại góc ban đầu bằng cách sử dụng hàm asin (arcsin):
math.asin(1.0471975511965976)Trong chế độ tương tác của Python, bạn có thể sử dụng toán tử gạch dưới _ để lấy kết quả của phép tính trước đó, giúp tiết kiệm thời gian gõ phím:
math.asin(_)Sau đó, bạn có thể chuyển đổi radian trở lại độ bằng hàm math.degrees():
math.degrees(_)Điều này sẽ đưa chúng ta trở lại giá trị góc ban đầu. Các hàm cos, acos, tan và atan cũng hoạt động theo nguyên lý tương tự.
Giải Phương Trình Đại Số và Hệ Phương Trình Tuyến Tính với SymPy và NumPy
Python không chỉ giới hạn ở các phép tính số học; nó còn có thể giải các phương trình đại số phức tạp nhờ các thư viện chuyên biệt. Bạn không cần đến các hệ thống đại số máy tính (CAS) độc quyền và đắt tiền như Mathematica hay Maple; Python là một giải pháp mã nguồn mở mạnh mẽ.
Giải Phương Trình Đại Số với SymPy
SymPy là một thư viện toán học tượng trưng cho Python, cho phép bạn làm việc với các biến số và biểu thức mà không cần gán giá trị cụ thể.
Hãy sử dụng SymPy để giải một phương trình đơn giản: 3x + 5 = 7. Mặc dù dễ dàng giải bằng tay, ví dụ này sẽ minh họa khả năng của SymPy.
Đầu tiên, nhập thư viện SymPy và định nghĩa biến x là một biến tượng trưng:
from sympy import *
x = symbols('x')SymPy thường mong đợi phương trình được đặt bằng 0. Chúng ta sẽ sử dụng hàm Eq() để biểu diễn phương trình:
eqn = Eq(3*x + 5, 7)
Minh họa việc giải một phương trình đại số đơn giản bằng thư viện SymPy trong môi trường Python
Bây giờ, sử dụng hàm solve() để tìm giá trị của x:
solve(eqn, x)Kết quả sẽ là 2/3.
Đối với các phương trình phức tạp hơn như phương trình bậc hai, SymPy vẫn có thể xử lý dễ dàng mà không yêu cầu bạn phải nhớ công thức nghiệm bậc hai. Ví dụ, giải phương trình x^2 + 4x + 2 = 0:
solve(x**2 + 4*x + 2, x)Các đáp án sẽ là 2 - căn(2) và 2 + căn(2). Lưu ý rằng bạn cần định nghĩa rõ ràng phép nhân, ví dụ 4*x thay vì 4x.
Nếu bạn sử dụng isympy từ dòng lệnh, nó sẽ tự động nhập SymPy, định nghĩa một số biến phổ biến như x, và thiết lập chế độ in đẹp để kết quả trông giống như trong sách giáo khoa.
Giải Hệ Phương Trình Tuyến Tính với NumPy
Thư viện NumPy là một công cụ xuất sắc để giải hệ phương trình tuyến tính, đặc biệt khi làm việc với ma trận.
Hãy giải hệ phương trình tuyến tính sau:
3x + 2y – z = 1
2x – 2y + 4z = -2
-x + 1/2y – z = 0
Chúng ta sẽ biểu diễn hệ phương trình này dưới dạng ma trận và vector. Điều quan trọng là các hệ số của biến, không phải chính các biến. Tạo một mảng 2 chiều (ma trận hệ số A) và một mảng khác cho vector hằng số (b) ở vế phải của hệ:
import numpy as np
A = np.array([[3, 2, -1], [2, -2, 4], [-1, 1/2, -1]])
b = np.array([1, -2, 0])Sau đó, sử dụng hàm linalg.solve() của NumPy để giải hệ (nếu hệ có nghiệm):
np.linalg.solve(A, b)
Cách giải một hệ phương trình tuyến tính phức tạp sử dụng thư viện NumPy trong Python, hiển thị ma trận và vector giải pháp
Bạn sẽ nhận được một danh sách các nghiệm cho hệ, trong trường hợp này là [1, -2, -2], tương ứng với các biến x, y, z.
Tính Toán Trung Bình, Trung Vị và Mode với Thư Viện Statistics
Nhiều máy tính khoa học và các phần mềm bảng tính như Excel có tích hợp các phép toán thống kê. Python cũng cung cấp một thư viện statistics để thực hiện các phép thống kê mô tả cơ bản một cách hiệu quả.
Đầu tiên, hãy tạo một tập dữ liệu ví dụ:
import statistics
data = [25, 42, 35, 25, 50]Để tính giá trị trung bình (mean) của tập dữ liệu:
statistics.mean(data)Để tính giá trị trung vị (median) – giá trị nằm ở giữa khi tập dữ liệu được sắp xếp:
statistics.median(data)Để tính mode – giá trị xuất hiện nhiều nhất trong tập dữ liệu:
statistics.mode(data)Trong ví dụ này, số 25 xuất hiện hai lần, là giá trị xuất hiện nhiều nhất. Nếu có nhiều giá trị có cùng tần suất xuất hiện cao nhất, hàm mode() sẽ trả về giá trị đầu tiên nó tìm thấy.
Minh họa các phép tính thống kê cơ bản như trung bình (mean), trung vị (median), và mode bằng module Statistics của Python
Tính Toán Giai Thừa, Hoán Vị và Tổ Hợp
Các phép toán tổ hợp cơ bản như giai thừa, hoán vị và tổ hợp cũng có sẵn trong Python, một lần nữa nhờ vào thư viện math.
Đầu tiên, hãy nhập các hàm cần thiết:
from math import factorial, comb, permGiai Thừa
Giai thừa của một số nguyên dương n, ký hiệu là n!, là tích của tất cả các số nguyên dương từ 1 đến n. Ví dụ, 49 giai thừa là 49!.
Để tính 49!:
factorial(49)Kết quả sẽ là một số rất lớn.
Tổ Hợp
Hàm comb(n, k) tính số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự (tổ hợp chập k của n). Ví dụ, để tính số tổ hợp có thể có khi rút 5 lá bài từ một bộ bài chuẩn 52 lá:
comb(52, 5)Hoán Vị
Hàm perm(n, k) tính số cách sắp xếp k phần tử từ n phần tử mà có quan tâm đến thứ tự (hoán vị chập k của n). Để tính hoán vị khi rút 5 lá bài từ bộ 52 lá (nơi thứ tự rút quan trọng):
perm(52, 5)Vẽ Đồ Thị Hàm Số với SymPy
SymPy không chỉ có khả năng giải phương trình mà còn có thể vẽ đồ thị các hàm số, tương tự như một chiếc máy tính đồ thị chuyên dụng. Điều này giúp trực quan hóa các mối quan hệ toán học một cách hiệu quả.
Bạn có thể vẽ đồ thị các hàm số có dạng y = mx + b, trong đó m là hệ số góc và b là điểm cắt trục y. Chúng ta chỉ cần phần mx + b. Ví dụ, để vẽ đồ thị hàm số y = 3x + 5:
from sympy import symbols, plot
x = symbols('x')
plot(3*x + 5)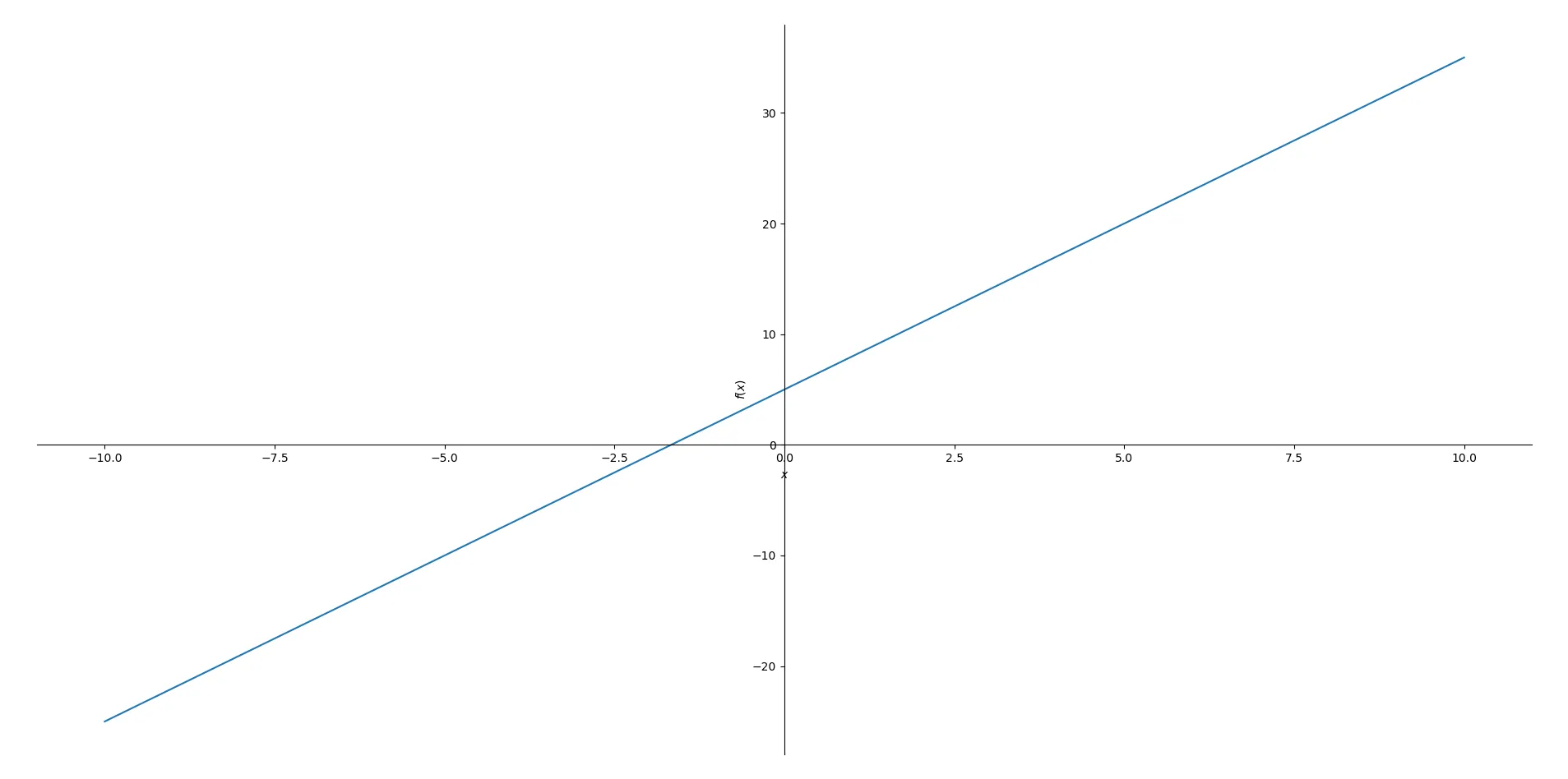
Kết quả đồ thị trực quan của một hàm số tuyến tính được tạo ra bởi thư viện SymPy trong Python
Một cửa sổ đồ thị sẽ bật lên hoặc đồ thị sẽ hiển thị trực tiếp trong môi trường Jupyter Notebook nếu bạn đang sử dụng.
Kết Luận
Python, với sự hỗ trợ đắc lực từ các thư viện mạnh mẽ như math, SymPy, NumPy và statistics, đã vượt xa vai trò của một ngôn ngữ lập trình thông thường để trở thành một “máy tính” đa năng và linh hoạt. Từ các phép tính số học cơ bản như lũy thừa, căn bậc N, logarit, đến các ứng dụng phức tạp hơn như giải phương trình đại số, hệ phương trình tuyến tính, thống kê mô tả, hoán vị, tổ hợp và thậm chí là vẽ đồ thị hàm số, Python đều có thể xử lý một cách hiệu quả và chính xác.
Khả năng tiếp cận miễn phí, mã nguồn mở, cùng với cộng đồng hỗ trợ lớn và tính linh hoạt cao, biến Python thành công cụ không thể thiếu cho sinh viên, nhà khoa học, kỹ sư và bất kỳ ai có nhu cầu làm việc với toán học và dữ liệu. Việc làm chủ những kỹ năng này không chỉ giúp bạn giải quyết các bài toán học một cách nhanh chóng mà còn mở ra cánh cửa đến với thế giới rộng lớn của khoa học dữ liệu, học máy và nghiên cứu khoa học. Hãy khám phá và tận dụng tối đa sức mạnh tính toán mà Python mang lại để nâng cao hiệu suất công việc và học tập của bạn.
Bạn có thể tham khảo thêm các bài viết khác của chúng tôi về ứng dụng của Python trong công nghệ tại trangtincongnghe.net!
